ITパスポート、基本情報技術者試験で問われる離散数学の基本と例題

ITパスポート

こんてんつ

ITパスポート、基本情報技術者試験で問われる離散数学の基本と、例題を列挙した。

  • 基数変換
  • 論理シフト、算術シフト
  • 過去問例題集

基礎

基数変換

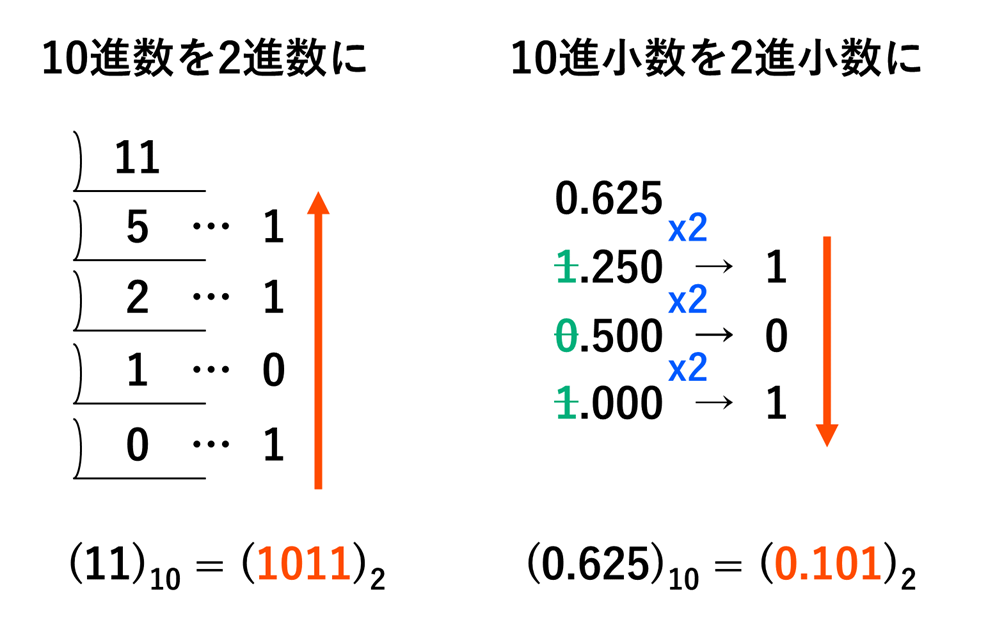
論理シフト、算術シフト

  • 論理シフト : 符号を考慮せず、2進数のビット列を左右にずらす。空いたビット列には0を入れる。
  • 算術シフト : 符号を考慮して、2進数のビット列を左右にずらす。左にずらす場合、符号ビットは動かさない。右にずらす場合、空いた場所には符号ビットと同じ値を入れる。

算術シフトで1左にずらすことは、2を掛けることを意味する。算術シフトで1右にずらすことは、2で割ることを意味する（切り上げ）。

過去問例題集

H27S

  • (0010\,1000) - 1は？

まず、

A : (0010\,1000) \\ B : (0000\,0001)

と置く。

- (0000\,0001) = (1111\,1110) + (0000\,0001) = (1111\,1111) \\

であり、

A - B = (0010\,1000) + (1111\,1111) = (1\,0010\,0111) = (0010\,0111)

となる。

H26A

  • 16進数における0.1を、10進数の分数で表すといくつか？
  • 16進数における0.01を、10進数の分数で表すといくつか？
  • 16進数における0.02を、10進数の分数で表すといくつか？
  • 16進数における0.05を、10進数の分数で表すといくつか？

それぞれ、次のようになる。

(0.1)_{16} = 1/16 \\ (0.01)_{16} = 1/256 \\ (0.02)_{16} = 2/256 \\ (0.05)_{16} = 5/256

H26A

  • 11進数で55500を10進数に変換するといくつか？

11進数の値×重みで求める。

\begin{eqnarray} &&11^4 \times 5 + 11^3 \times 5 + 11^2 \times 5 + 11^1 \times 5 + 11^0 \times 5 \\ &=& 73205 + 6655 + 605 + 55 + 0 \\ &=& 80520 \end{eqnarray}

H26S

2進小数は10進小数で次のように表す。

(0.1)_{2} = 0.5 \\ (0.01)_{2} = 0.25 \\ (0.001)_{2} = 0.125 \\ (0.0001)_{2} = 0.0625

これの組み合わせで表現できるか否かで判断する。

例えば、

  • 10進小数の0.375は2進小数で0.25+0.125であり有限小数。
  • 10進小数の0.05は上の2進小数の組み合わせで表現できないので無限小数。

もしくは、愚直にたすき算にて10進小数→2進小数と表してみて判断する。

H24S

  • 10進数における0.3を、8進数で表すといくつか？
  • 10進数における0.4を、8進数で表すといくつか？
  • 10進数における0.5を、8進数で表すといくつか？

たすき算にて求める。

(0.3) _ {10} = (0.23146) _ {8} \\ (0.4) _ {10} = (0.3146) _ {8} \\ (0.5) _ {10} = (0.4) _ {8}

となる。

H24A

  • 1101\, 0000を右に2ビット算術シフトせよ。

右にシフトした後、空いた場所には符号ビットと同じ値を入れる

(1101\,0000) -> (1111\,0100)

の様になる。

  • (0001\, 0100) _ 2 - (1111\, 0100) _ 2は？

まず、

A : 0001\, 0100 \\ B : 1111\,0100

と置く。

- (1111\, 0100) = (0000\,1011) + (0000\,0001) = (0000\,1100) \\

であり、

A - B = (0001\, 0100) + (0000\,1100) = (0010\,0000)

となる。

H24S

  • (0000\,1000) _ {2}を3倍せよ。

1ビットだけ左にシフト(×2)してできるビット列に対して元のビット列の加算(＋1)するという処理を組み合わせることで、3倍にする演算を行う。

(0000\,1000) _ {2} \times 3 = (0001\,0000) _ {2} + (0000\,1000) _ {2} = (0001\,1000) _ {2}