こんてんつ

連続体力学を学ぶ上で重要なコーシーの応力テンソルを導出する。一般的な書物は3次元からの誘導が殆どである。ここでは理解しやすい2次元問題からの導出を実施し、その後3次元問題でも導出する。

コーシーの応力テンソルの意味

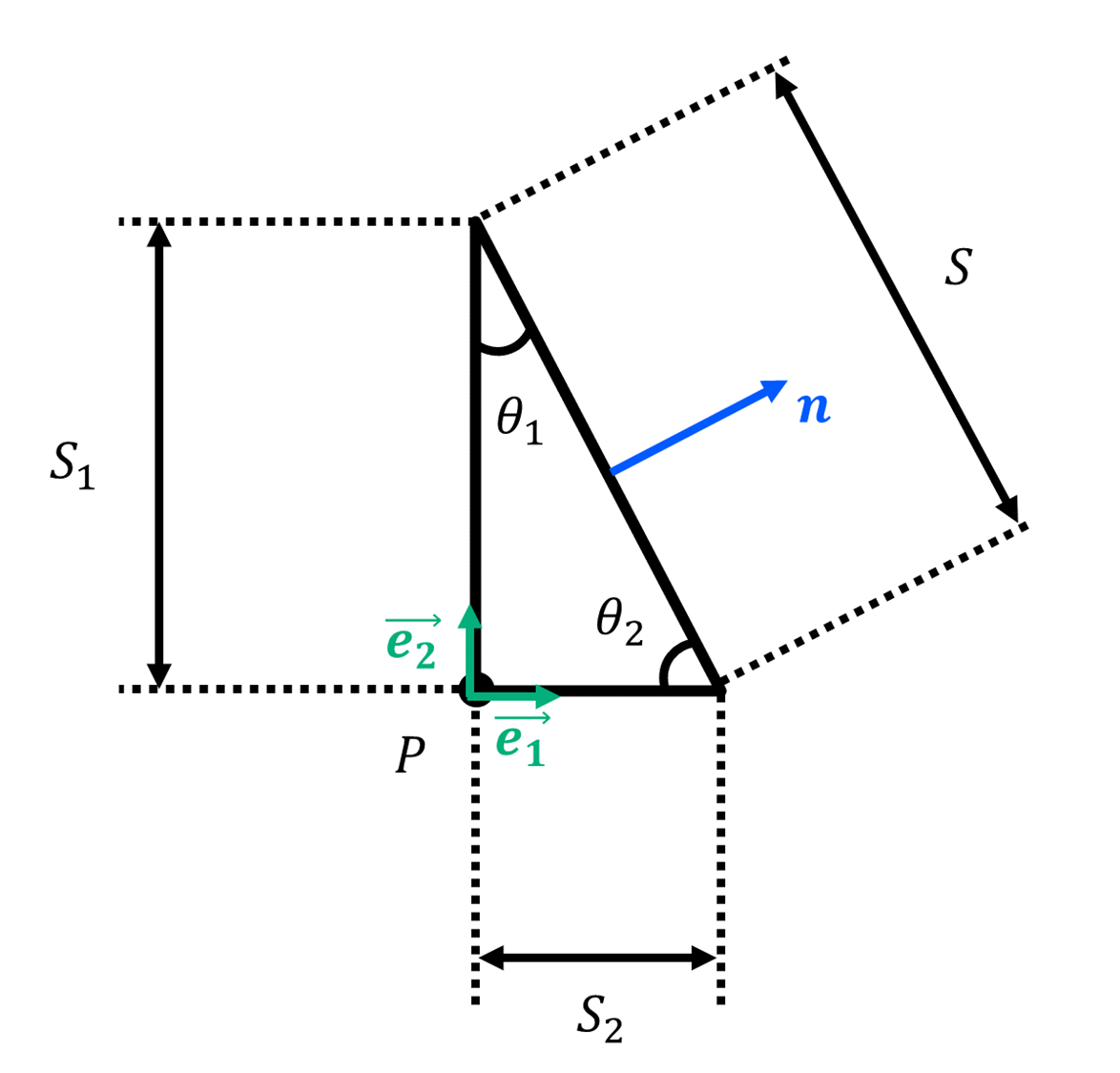
次の様な任意形状の物体を考えた時、コーシーの応力テンソル $\boldsymbol{\sigma}$ が分かれば、任意の $\boldsymbol{n}$ 面に作用する点 $P$ を通る表面力ベクトル $\boldsymbol{t}$ が分かる（ $\boldsymbol{t}=\boldsymbol{\sigma}\boldsymbol{n}$ ）という代物のことである。

2次元問題

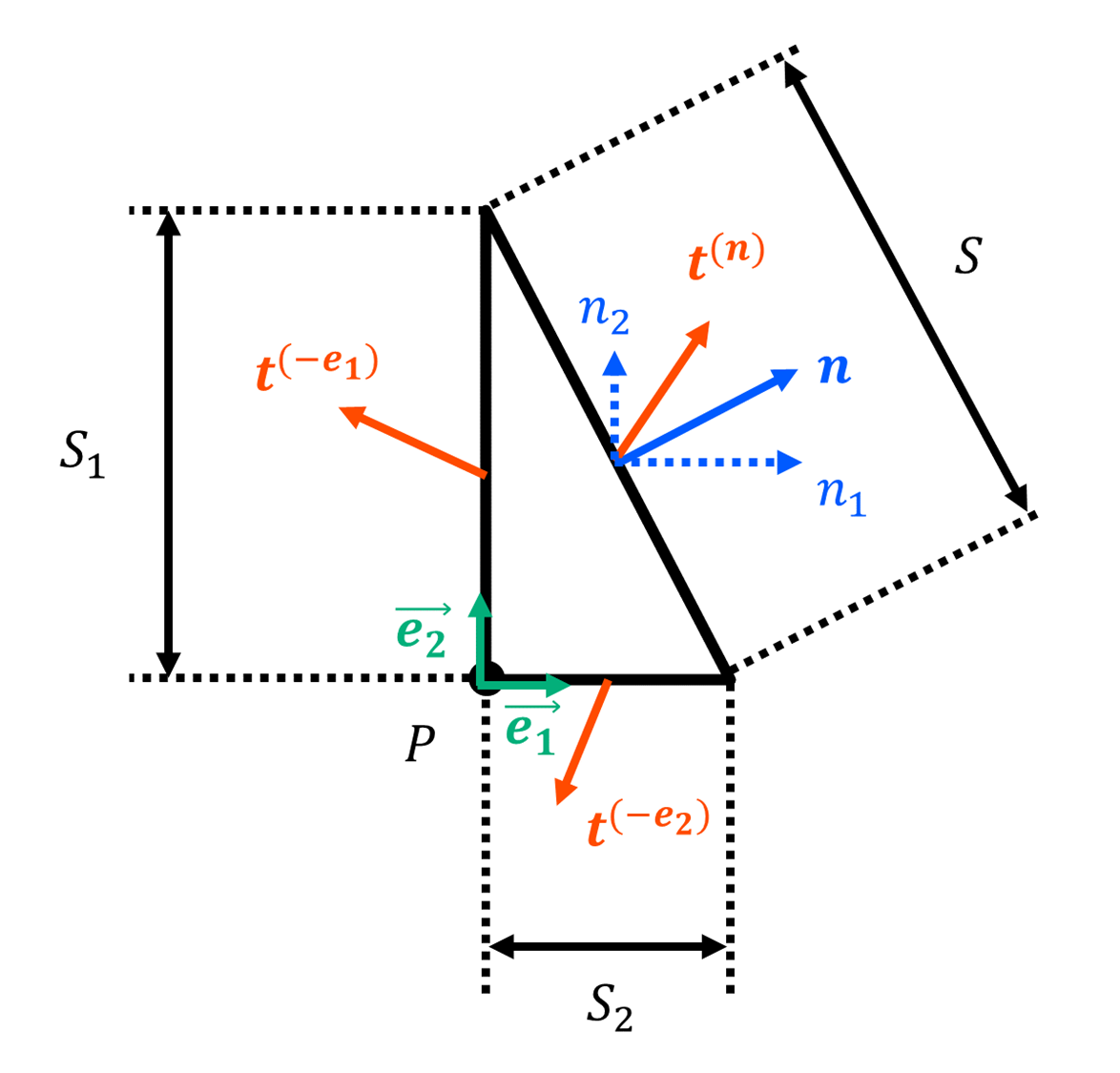
下記の様な点 $P$ 近傍の微小三角形を考える。この三角形それぞれの面（辺）に現れる表面力ベクトルを考える。それらは次のようになる。

$\boldsymbol{n}$ を単位法線ベクトルとした面（辺）に現れる表面力ベクトルを $\boldsymbol{t}^{(n)}$
$-\boldsymbol{e} _ 1$ を単位法線ベクトルとした面（辺）に現れる表面力ベクトルを $\boldsymbol{t}^{(-\boldsymbol{e} _ 1)}$
$-\boldsymbol{e} _ 2$ を単位法線ベクトルとした面（辺）に現れる表面力ベクトルを $\boldsymbol{t}^{(-\boldsymbol{e} _ 2)}$

とする。ここで、

ベクトル $\boldsymbol{ n }$ に垂直なの辺の長さを $S$
$\boldsymbol{e} _ 1$ に垂直な辺の長さを $S _ 1$
$\boldsymbol{e} _ 2$ に垂直な辺の長さを $S _ 2$

とする。三角形に作用する力のつり合い式より、

$\displaystyle \boldsymbol{t}^{(\boldsymbol{n})} S + \boldsymbol{t}^{(-\boldsymbol{e} _ 1)} S_1 + \boldsymbol{t}^{(-\boldsymbol{e} _ 2)} S_2 = 0$

を得る。ところで、 $\boldsymbol{t}^{(-\boldsymbol{e} _ 1)} = -\boldsymbol{t}^{(\boldsymbol{e} _ 1)}$ 、 $\boldsymbol{t}^{(-\boldsymbol{e} _ 2)} = -\boldsymbol{t}^{(\boldsymbol{e} _ 2)}$ であるから、

$\displaystyle \boldsymbol{t}^{(\boldsymbol{n})} S - \boldsymbol{t}^{(\boldsymbol{e} _ 1)} S_1 - \boldsymbol{t}^{(\boldsymbol{e} _ 2)} S_2 = 0$

となる。ここで、次の図の様に

$\displaystyle \begin{eqnarray} S_1 = S cos \theta_1 \\ S_2 = S cos \theta_2 \end{eqnarray}$

であるが、ベクトル内積の公式（正射影の公式）より

$\displaystyle \begin{eqnarray} && cos \theta_1 = \frac{\vec{n} \cdot \vec{e_1}}{|\vec{n}||\vec{e_1}|} = \frac{\vec{n} \cdot \vec{e_1}}{|1||1|} = \vec{n} \cdot \vec{e_1}\\ && cos \theta_2 = \frac{\vec{n} \cdot \vec{e_2}}{|\vec{n}||\vec{e_2}|} = \frac{\vec{n} \cdot \vec{e_2}}{|1||1|} = \vec{n} \cdot \vec{e_2} \end{eqnarray}$

なので、

$\displaystyle \begin{eqnarray} S_1 = S (\boldsymbol{n} \cdot \boldsymbol{e}_1) \\ S_2 = S (\boldsymbol{n} \cdot \boldsymbol{e}_2) \end{eqnarray}$

となる。よってつり合いの式は、

$\displaystyle \boldsymbol{t}^{(\boldsymbol{n})} S - \boldsymbol{t}^{(\boldsymbol{e} _ 1)} S (\boldsymbol{n} \cdot \boldsymbol{e}_1) - \boldsymbol{t}^{(\boldsymbol{e} _ 2)} S (\boldsymbol{n} \cdot \boldsymbol{e}_2) = 0$

となる。 $S$ で除せば、

$\displaystyle \boldsymbol{t}^{(\boldsymbol{n})} - \boldsymbol{t}^{(\boldsymbol{e} _ 1)} (\boldsymbol{n} \cdot \boldsymbol{e}_1) - \boldsymbol{t}^{(\boldsymbol{e} _ 2)} (\boldsymbol{n} \cdot \boldsymbol{e}_2) = 0$

となる。この式は、点 $P$ を通る $e _ 1$ 、 $e _ 2$ 軸に垂直な表面ベクトルを調べておけば、任意の法線ベクトル $\boldsymbol{n}$ を持つ面の表面力ベクトル $\boldsymbol{t}^{(\boldsymbol{n})}$ を求めることが出来るということを表す。ここで法線ベクトル $\boldsymbol{n}$ を $\boldsymbol{e} _ 1$ 、 $\boldsymbol{e} _ 2$ の成分で表し、

$\displaystyle \boldsymbol{t}^{(\boldsymbol{n})} - \boldsymbol{t}^{(\boldsymbol{e} _ 1)} n_1 - \boldsymbol{t}^{(\boldsymbol{e} _ 2)} n_2 = 0$

より、

$\displaystyle \boldsymbol{t}^{(\boldsymbol{n})} = \boldsymbol{t}^{(\boldsymbol{e} _ 1)} n_1 + \boldsymbol{t}^{(\boldsymbol{e} _ 2)} n_2$

を得る。さて、最後に、すべての表面力ベクトルを $\boldsymbol{e} _ 1$ 、 $\boldsymbol{e} _ 2$ の成分で表し、つり合いの式を書き換えると、

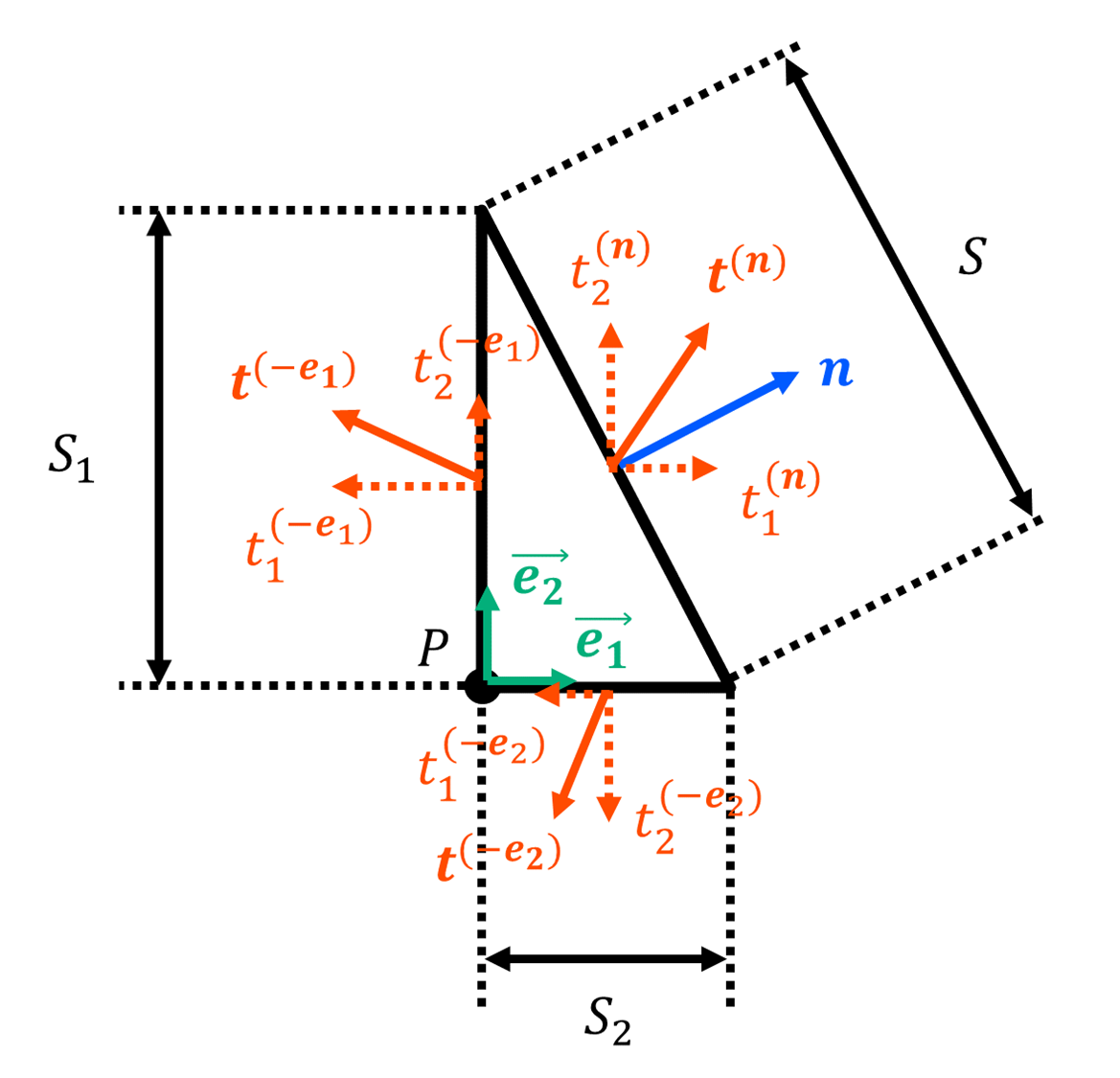
$\displaystyle \begin{eqnarray} \begin{Bmatrix} t^{(\boldsymbol{n})}_1 \\ t^{(\boldsymbol{n})}_2 \end{Bmatrix} &=& \begin{Bmatrix} t^{(\boldsymbol{e} _ 1)}_1 \\ t^{(\boldsymbol{e} _ 1)}_2 \end{Bmatrix} n_1 + \begin{Bmatrix} t^{(\boldsymbol{e} _ 2)}_1 \\ t^{(\boldsymbol{e} _ 2)}_2 \end{Bmatrix} n_2 \\ &=& \begin{bmatrix} t^{(\boldsymbol{e} _ 1)}_1 & t^{(\boldsymbol{e} _ 2)}_1\\ t^{(\boldsymbol{e} _ 1)}_2 & t^{(\boldsymbol{e} _ 2)}_2 \end{bmatrix} \begin{Bmatrix} n_1 \\ n_2 \end{Bmatrix} \end{eqnarray}$

の様になる。この式に現れている行列こそコーシーの応力テンソルである。 $\boldsymbol{t}=\boldsymbol{\sigma}\boldsymbol{n}$ の様にコーシーの応力テンソル $\boldsymbol{\sigma}$ が分かれば、任意の $\boldsymbol{n}$ 面に作用する点 $P$ を通る表面力ベクトル $\boldsymbol{t}$ が分かる。

3次元問題

下記の様な点 $P$ 近傍の微小四面体を考える。この四面体それぞれの面に現れる表面力ベクトルを考える。それらは次のようになる。

$\boldsymbol{n}$ を単位法線ベクトルとした面に現れる表面力ベクトルを $\boldsymbol{t}^{(n)}$
$-\boldsymbol{e} _ 1$ を単位法線ベクトルとした面に現れる表面力ベクトルを $\boldsymbol{t}^{(-\boldsymbol{e} _ 1)}$
$-\boldsymbol{e} _ 2$ を単位法線ベクトルとした面に現れる表面力ベクトルを $\boldsymbol{t}^{(-\boldsymbol{e} _ 2)}$
$-\boldsymbol{e} _ 3$ を単位法線ベクトルとした面に現れる表面力ベクトルを $\boldsymbol{t}^{(-\boldsymbol{e} _ 3)}$

とする。ここで、

ベクトル $\boldsymbol{ n }$ に垂直な面の面積を $\Delta S$
$\boldsymbol{e} _ 1$ に垂直な面の面積を $\Delta S _ 1$
$\boldsymbol{e} _ 2$ に垂直な面の面積を $\Delta S _ 2$
$\boldsymbol{e} _ 3$ に垂直な面の面積を $\Delta S _ 3$

とする。三角形に作用する力のつり合い式より、

$\displaystyle \boldsymbol{t}^{(\boldsymbol{n})} \Delta S + \boldsymbol{t}^{(-\boldsymbol{e} _ 1)} \Delta S_1 + \boldsymbol{t}^{(-\boldsymbol{e} _ 2)} \Delta S_2 + \boldsymbol{t}^{(-\boldsymbol{e} _ 3)} \Delta S_3 = 0$

$\displaystyle \boldsymbol{t}^{(\boldsymbol{n})} \Delta S - \boldsymbol{t}^{(\boldsymbol{e} _ 1)} \Delta S_1 - \boldsymbol{t}^{(\boldsymbol{e} _ 2)} \Delta S_2 - \boldsymbol{t}^{(\boldsymbol{e} _ 3)} \Delta S_3 = 0$

となる。ここで、正射影の公式より、

$\displaystyle \begin{eqnarray} \Delta S_1 = \Delta S (\boldsymbol{n} \cdot \boldsymbol{e}_1) \\ \Delta S_2 = \Delta S (\boldsymbol{n} \cdot \boldsymbol{e}_2) \\ \Delta S_3 = \Delta S (\boldsymbol{n} \cdot \boldsymbol{e}_3) \end{eqnarray}$

となるので、つり合いの式は、

$\displaystyle \boldsymbol{t}^{(\boldsymbol{n})} \Delta S - \boldsymbol{t}^{(\boldsymbol{e} _ 1)} \Delta S (\boldsymbol{n} \cdot \boldsymbol{e}_1) - \boldsymbol{t}^{(\boldsymbol{e} _ 2)} \Delta S (\boldsymbol{n} \cdot \boldsymbol{e}_2) - \boldsymbol{t}^{(\boldsymbol{e} _ 3)} \Delta S (\boldsymbol{n} \cdot \boldsymbol{e}_3) = 0$

となる。 $\Delta S$ で除せば、

となる。この式は、点 $P$ を通る $e _ 1$ 、 $e _ 2$ 、 $e _ 3$ 軸に垂直な表面ベクトルを調べておけば、任意の法線ベクトル $\boldsymbol{n}$ を持つ面の表面力ベクトル $\boldsymbol{t}^{(\boldsymbol{n})}$ を求めることが出来るということを表す。ここで法線ベクトル $\boldsymbol{n}$ を $\boldsymbol{e} _ 1$ 、 $\boldsymbol{e} _ 2$ 、 $\boldsymbol{e} _ 3$ の成分で表し、

$\displaystyle \boldsymbol{t}^{(\boldsymbol{n})} - \boldsymbol{t}^{(\boldsymbol{e} _ 1)} n_1 - \boldsymbol{t}^{(\boldsymbol{e} _ 2)} n_2 - \boldsymbol{t}^{(\boldsymbol{e} _ 3)} n_3 = 0$

より、

$\displaystyle \boldsymbol{t}^{(\boldsymbol{n})} = \boldsymbol{t}^{(\boldsymbol{e} _ 1)} n_1 + \boldsymbol{t}^{(\boldsymbol{e} _ 2)} n_2 + \boldsymbol{t}^{(\boldsymbol{e} _ 3)} n_3$

を得る。さて、最後に、すべての表面力ベクトルを $\boldsymbol{e} _ 1$ 、 $\boldsymbol{e} _ 2$ 、 $\boldsymbol{e} _ 3$ の成分で表し、つり合いの式を書き換えると、

$\displaystyle \begin{eqnarray} \begin{Bmatrix} t^{(\boldsymbol{n})}_1 \\ t^{(\boldsymbol{n})}_2 \\ t^{(\boldsymbol{n})}_3 \end{Bmatrix} &=& \begin{Bmatrix} t^{(\boldsymbol{e} _ 1)}_1 \\ t^{(\boldsymbol{e} _ 1)}_2 \\ t^{(\boldsymbol{e} _ 1)}_3 \end{Bmatrix} n_1 + \begin{Bmatrix} t^{(\boldsymbol{e} _ 2)}_1 \\ t^{(\boldsymbol{e} _ 2)}_2 \\ t^{(\boldsymbol{e} _ 2)}_3 \end{Bmatrix} n_2 + \begin{Bmatrix} t^{(\boldsymbol{e} _ 3)}_1 \\ t^{(\boldsymbol{e} _ 3)}_2 \\ t^{(\boldsymbol{e} _ 3)}_3 \end{Bmatrix} n_3 \\ &=& \begin{bmatrix} t^{(\boldsymbol{e} _ 1)}_1 & t^{(\boldsymbol{e} _ 2)}_1 & t^{(\boldsymbol{e} _ 3)}_1\\ t^{(\boldsymbol{e} _ 1)}_2 & t^{(\boldsymbol{e} _ 2)}_2 & t^{(\boldsymbol{e} _ 3)}_2\\ t^{(\boldsymbol{e} _ 1)}_3 & t^{(\boldsymbol{e} _ 2)}_3 & t^{(\boldsymbol{e} _ 3)}_3 \end{bmatrix} \begin{Bmatrix} n_1 \\ n_2 \\ n_3 \end{Bmatrix} \end{eqnarray}$

こんてんつこうかい

コーシーの応力テンソルの導出（2次元と3次元）

こんてんつ

コーシーの応力テンソルの意味

2次元問題

3次元問題